Twelve Times Tables Test
Shuhaimie | 09:38 | 12 Test | 0 comments
What About the 12 Times Table?
Shuhaimie | 09:32 | 12 Times | 0 comments
Sounds tough, but once you have mastered the 10× table, it is just a few steps away.
| Firstly, 11× is mostly easy: from 11×2 to 11×9 you just put the two digits together. 11×2=22, 11×3=33, ..., 11×9=99. | ||
And of course 2×, 5× and 10× just follow their simple rules you know already, so it just leaves these to remember:
| ||
And the "Big 3":
|
Math Trainer - Multiplication
Shuhaimie | 01:26 | Trainer | 1 comments
Get in some serious multiplication table training. Responds to your answers ... so it will train your weaknesses. Use 3 sessions of 5 minutes each per day for best results.
Train yourself to REMEMBER, don't calculate.
Features of the Math Trainer
| Breaks the 10× table into 4 "chunks" (5×, 6×6 to 9×9, etc) so that you can concentrate on getting good one chunk at a time. | |
| Designed for high speed so that you get lots of practice | |
| Remembers your performance (during the session, but not between sessions) so that it gives you more practice on your weaknesses. | |
| Shows you the correct answer if you get it wrong | |
| Timed Workout style just like an athlete would use |
Timing
If you just want to practice at your own pace, choose "0" minutes, and press "Stop" when you are done.Tips 1 : Order Does Not Matter
Shuhaimie | 18:09 | Tips | 0 comments
When you multiply two numbers, it does not matter which is first or second, the answer is always the same.
| In fact, it is like half of the table is a mirror image of the other! So, don't memorise both "3×5" and "5×3", just memorise that "a 3 and a 5 make 15" when multiplied. This is very important! It nearly cuts the whole job in half. | 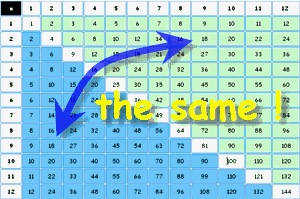 |
In your mind you should think of so you should be thinking something like this:3 and 5 "together" making 15. | 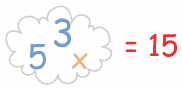 |
Multiplication Tables
Shuhaimie | 08:31 | Tables | 0 comments
How to Learn:
 | Your life will be a lot easier when you can simply remember the multiplication tables. So ... train your memory! First, use the table above to start putting the answers into your memory. |
Kuiz Matematik
Shuhaimie | 09:05 | Kuiz | 0 comments
| Selesaikan: | ||
Jawab di sini: | ||
| Markah: | ||
Sifir
Shuhaimie | 04:32 | Sifir | 0 comments
Sifir adalah salah satu cara untuk memudahkan kita mengingati jumlah hasil darab sesuatu nombor. Walaupun sifir dapat membantu kita menyelesaikan masalah berkaitan pendaraban, konsep utama proses pendaraban perlu sentiasa diingat bagi membantu kefahaman untuk penyelesaian masalah yang lebih rumit.
Untuk penguasaan kemahiran mendarab, sifir yang perlu diingat adalah sifir 1 hingga ke sifir 9. Bagi hasil darab untuk nombor yang lebih besar kemahiran-kemahiran pendaraban perlu dikuasai dengan baik.
Perlu diingat;
1 × 10 = 10
10 × 10 = 100
10 × 100 = 1000
100 × 100 = 10,000
1000 × 1000 = 1,000,000
Ini bermakna;
8 × 10 = 80
16 × 100 = 1,600
241 × 1,000 = 241,000
Sebelum kita meneruskan contoh-contoh latihan operasi darab untuk nombor-nombor yang lebih besar mari kita lihat Jadual Sifir di bawah:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | x |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 2 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 3 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 4 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 5 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 6 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 7 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 8 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 9 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 10 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 11 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 12 |
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | x |
Operasi Darab
Shuhaimie | 04:21 | Darab | 0 comments
Operasi darab merupakan operasi yang paling menyeronokkan kerana dalam proses penyelesaian masalah semasa membuat operasi darab pelbagai kaedah boleh digunakan serentak. Ini dapat melatih anda dalam membuat penilaian tentang sesuatu kaedah yang bersesuaian dengan bentuk soalan.
Untuk itu, Operasi Darab ini diberikan penekanan utama dalam melatih kreativiti dan kemahiran berfikir. Adalah dinasihatkan agar semua pelajar memberi tumpuan sepenuhnya kepada topik ini.
Proses pendaraban merupakan operasi yang penting dan mempunyai kaitan yang rapat dengan operasi tambah. Pendaraban sebenarnya adalah proses penambahan sesuatu angka yang sama secara berulang-ulang.
Contoh: Nombor 8 dicampur sebanyak 4 kali,
Ini boleh ditulis; 8 + 8 + 8 + 8 = 32
Atau 8 × 4 = 32
Bayangkan sekotak limau yang mengandungi 7 biji buah limau. Sekiranya seorang penjual buah menjual 7 kotak buah limau sehari, berapa biji buah limau yang telah dijualnya?
Penyelesaian;
Sekotak Limau = 7 biji
Bilangan Kotak Dijual = 7 kotak
Jumlah Buah Limau = 7 + 7 + 7 + 7 + 7 + 7 + 7
= 49 Biji Buah Limau
Atau = 7 × 7 = 49
Operasi Arithmetik
Shuhaimie | 08:11 | Arithmetik | 0 comments
Penambahan (+)
Operasi ini mencampurkan dua nombor (atau lebih) kepada satu nombor baru iaitu jumlah.Penolakan (-)
Penolakan merupakan operasi songsang penambahan. Hasil penolakan, iaitu perbezaan merupakan hasil tolakan subtrahend dari minuend. Kalau nilai minuend lebih besar daripada subtrahend, perbezaan akan menjadi nomobr positif, dan vice versa. Kalau minuend sama dengan subtrahend, perbezaan akan menjadi sifar.Pendaraban (×)
Pendaraban merupakan penambahan berkali-kali. Pendaraban antara dua nombor, dipanggil faktor menghasilkan hasil darab. Indentiti pendaraban ialah nombor 1, kerana apa-apa nombor yang didarab dengan 1 akan menghasilkan nombor itu yang sama.Pembahagian (÷)
Pembahagiab pula merupakan songsang operasi pendaraban. Pembahagian satu nombor oleh satu nombor yang lain menghasiklan hasil darab. Pembahagian sesuatu nombor oleh nombor sifar akan menghasilkan nombor tak tertakrif.Lain
Operasi aritmetik lain termasuk peratus, punca kuasa dua, pengeksponenan, dan fungsi logaritma.Welcome!
Shuhaimie | 03:47 | welcome | 0 comments
Welcome to my blog. This blog was build to fullfill my semester assignment. Thank you for your interest....
Nama Penuh : Mohd Shuhaimie B Rani
No Matrik : D20102042168
Topik : Matematik - Operasi Darab


